Research
Analysis of Dynamical Systems
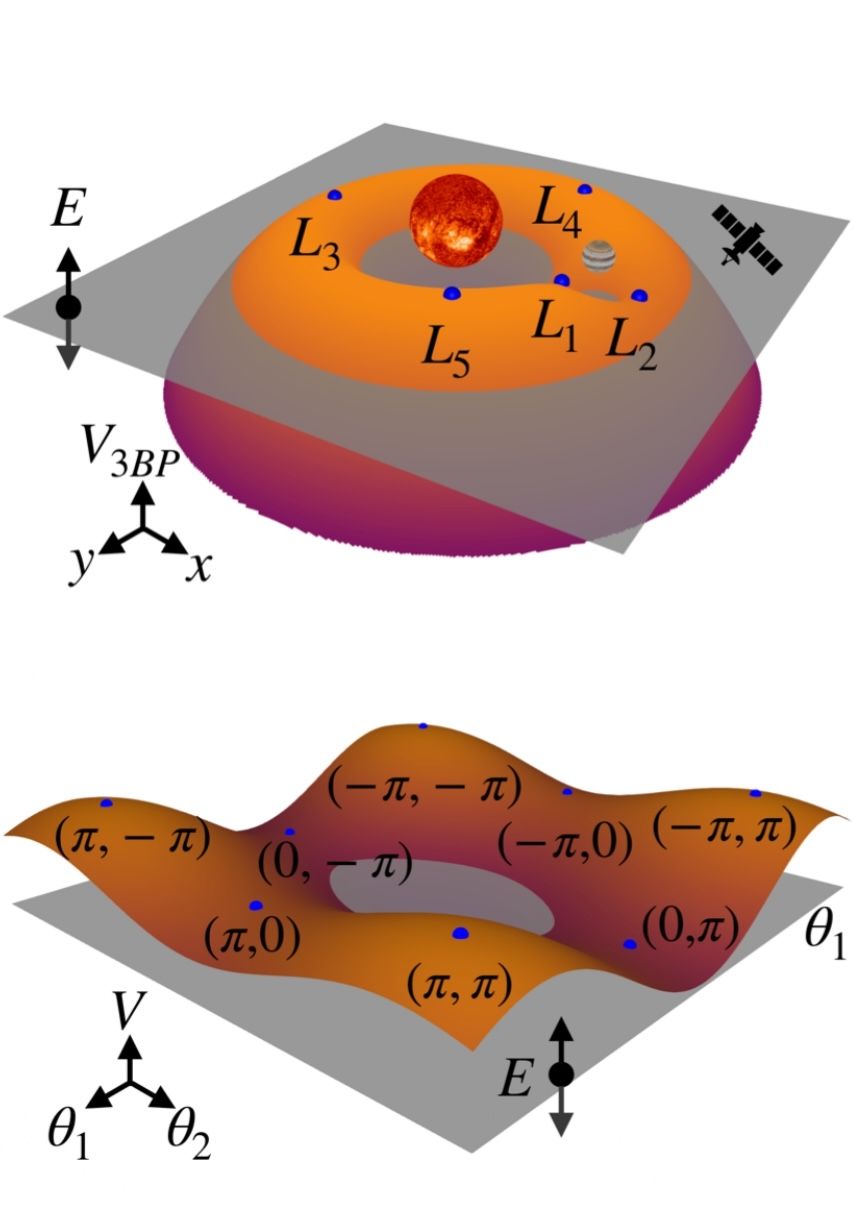
In the broadest sense, my interests in mathematics lie in the analysis of dynamical systems. This is an all-encompasing term to mean that I am interested in equations that change with either a discrete or a continuous 'time' variable, and can be either deterministic or stochastic. I have a particular focus on understanding complex pattern-forming behaviour, typically in the form of nonlinear waves and coherent structures in spatially-extended systems, including, but not limited to, partial differential equations, non-local equations, and spatially-discrete lattice dynamical systems. Examples of waves and patterns that I continue to focus my research on are spiral waves, spatially-localized steady-states (see below), and spatio-temporal chaotic attractors.
My approach brings together tools from real and functional analysis, graph theory, topology, and geometry, and unites them with state-of-the-art computational methods, such as semi-definite programming, machine learning, and computer-assisted proofs. It is through this unification of computation and analysis that my work also seeks to develop computational tools that are motivated by the theory I have developed over my career as a dynamical systems analyst.
Data-Driven Discovery of Mappings
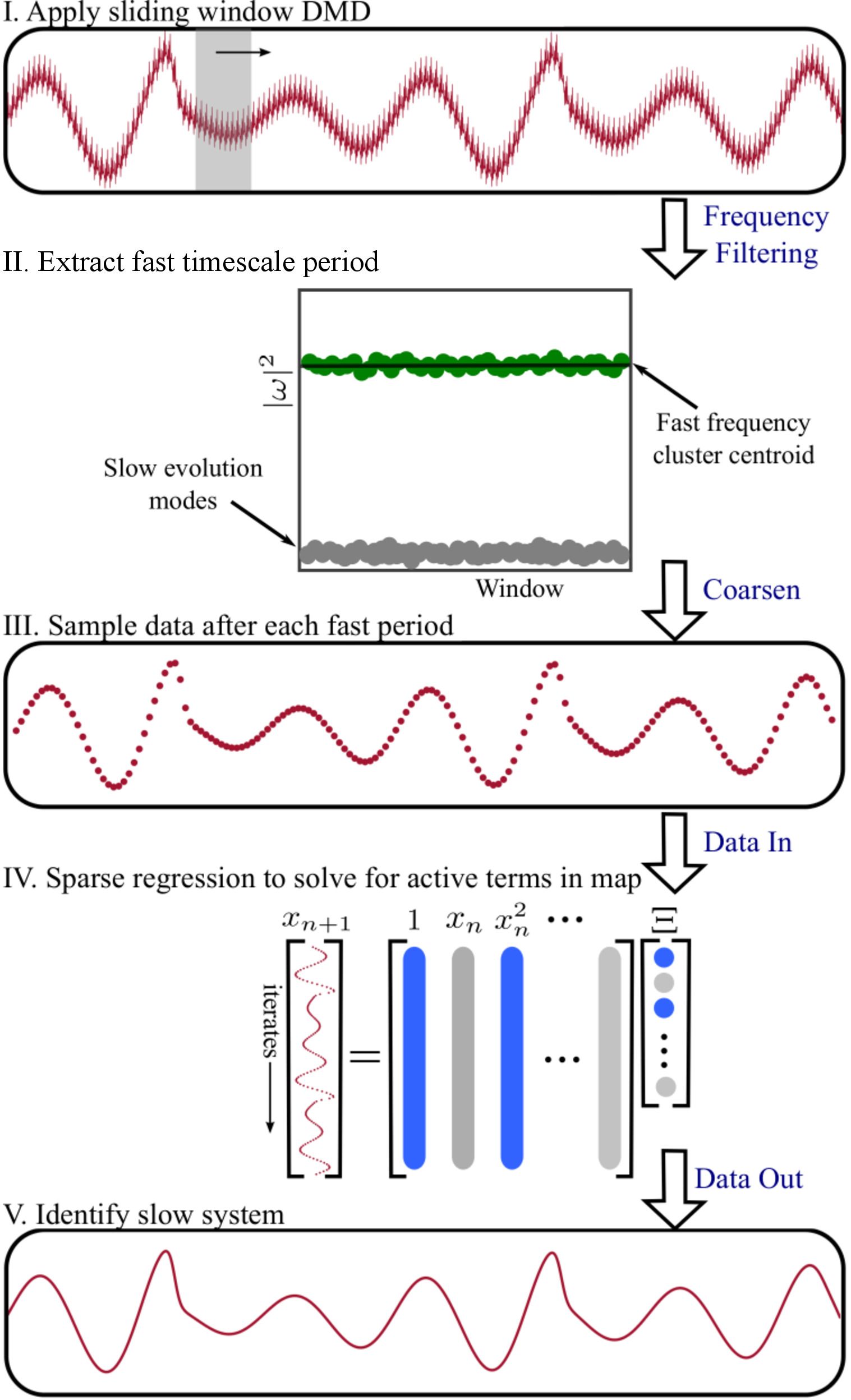
With the increasing size of experimental datasets and continual advancement of computational techniques, there is a growing demand for data-driven techniques for analyzing and forecasting dynamical systems which model these datasets. My work proposes a method of data-driven discovery of Poincaré maps based upon sparse regression techniques, specifically the sparse identification of nonlinear dynamics (SINDy) algorithm. This method can be applied to determine the dynamics on and near invariant manifolds of a given dynamical system, as well as provide long-time forecasting of the coarse-grained dynamics of multiscale systems.
Myself and my collaborators have also used this work to create a data-driven method for averaging of multiscale phenomena that evolve on multiple distinct timescales which are so prevalent throughout the sciences. A simple example of this would be the tides where high and low tide come at a regular period of approximately half a day, while the influence of the sun's gravity creates a slow drift in this almost periodic phenomena which can only be observed on long timescales. As in the tidal example, it is often the case with such multiscale phenomena that the governing equations of the persistent and approximately periodic fast scales are prescribed, while the emergent slow scale evolution is unknown. Our work presents an accurate and efficient method for extracting the slow timescale dynamics from signals exhibiting multiple timescales. A visual summary of the algorithm is provided on the left, while an accessible overview of this method can be found in this video.
Polynomial Optimization for Dynamical Systems Analysis
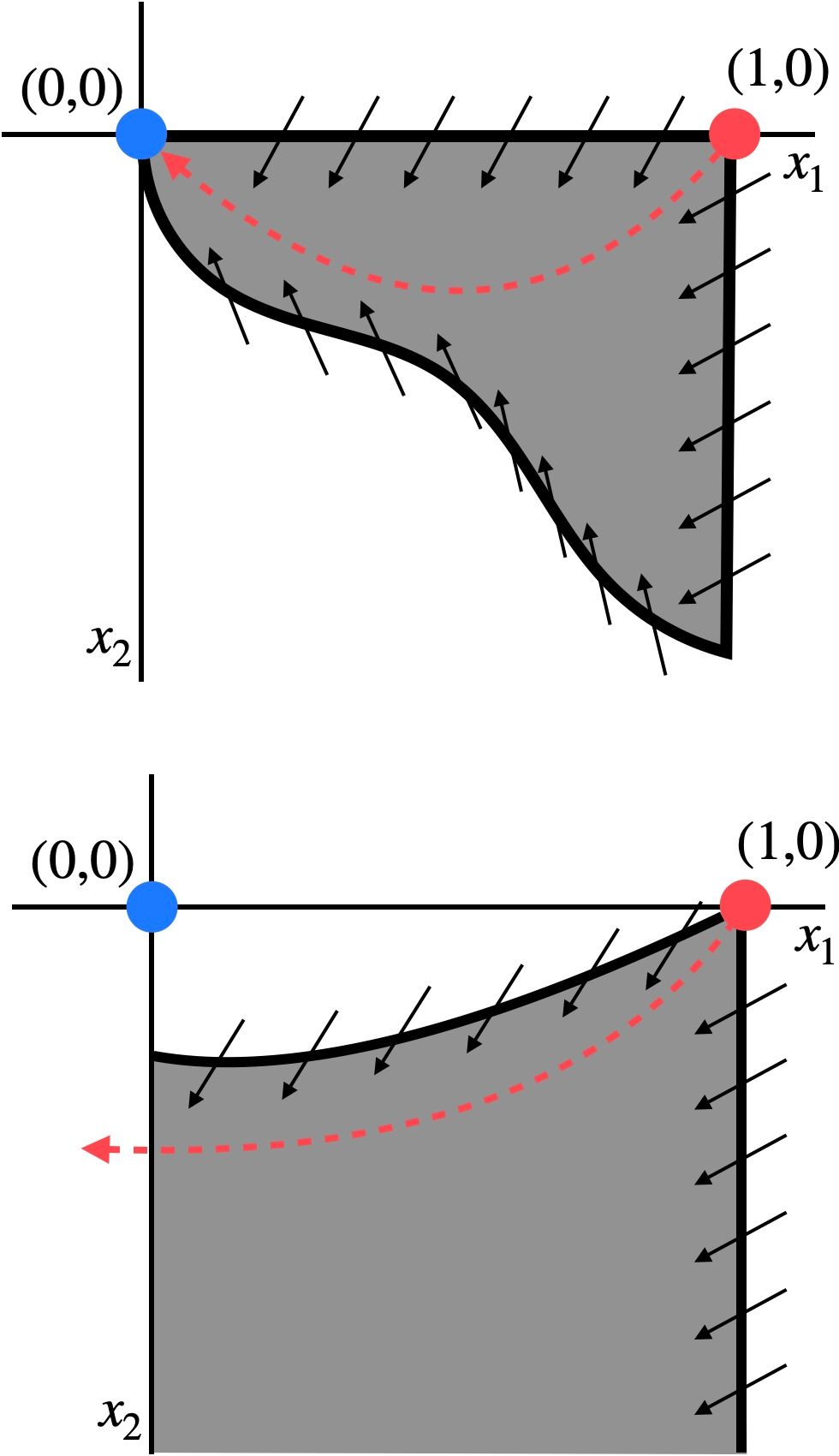
Many important statements about ODEs and PDEs can be proved by finding auxiliary functions. These are scalar-valued functions whose time evolution along trajectories obeys certain pointwise inequalities that imply the desired result. A familiar example is a Lyapunov function, which is used to prove stability of a state by showing that it is positive and decreasing in time along trajectories near the state. Finding such functions can be a tremendously rewarding task, but it is typically difficult as there are no general methods to guide construct them analytically.
When the ODE in question is polynomial one can attempt to find auxiliary functions by expanding them in a monomial basis, giving that the required inequalities amount to tuning the coefficients of the auxiliary function to guarantee nonnegativity of a polynomial expression on a specified set. Although deciding nonnegativity of a multivariable polynomial is NP-hard in general, nonnegativity can be replaced by the stronger but more tractable condition that the polynomial admits a representation as a sum of squares (SOS). The resulting SOS-constrained problem can be solved computationally by reformulating it as a semidefinite program and solving the latter numerically, giving the coefficients of the auxiliary function.
My own work in this area has applied these computational techniques to creating trapping bariers in phase space that can be used to infer the existence and non-existence of heteroclinic orbits. This work was used to improve upon my analysis on an FKPP-Burgers system, and insight gained from its application led to me proving the exact value of the minimum wave speed in Keller-Segel models for chemotaxis. Recently I have been working to extend computational SOS methods to problems in the calculus of variations, motivated by problems in partial differential equations, and to system analysis from data using the Koopman operator.
Localized Pattern Formation
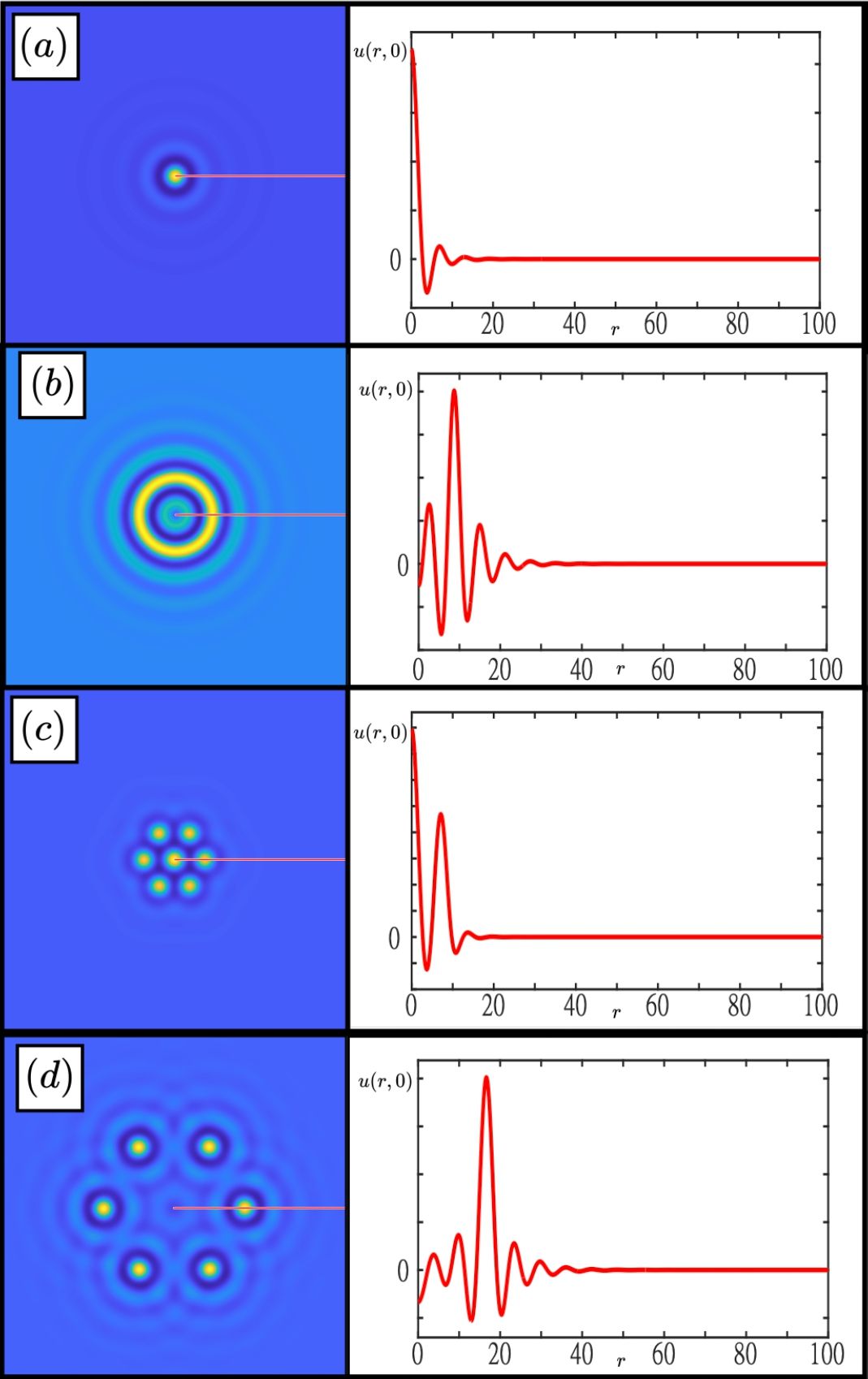
Spatially localized patterns have been observed in a wide variety of physical situations, ranging from vegetation patterns to crime hotspots to chemical concentration patterns. As solutions to partial differential equations such spatially localized patterns often exhibit exotic bifurcation structures. In particular, the Swift-Hohenberg equation is a widely studied partial differential equation which is known to support a variety of spatially localized structures, and in one spatial dimension the Swift-Hohenberg equation exhibits spatially localized steady-state solutions which give way to a bifurcation structure known as snaking. That is, spatially-localized solutions bounce between two different values of the bifurcation parameter while ascending in norm and retaining the same basic shape.
Here my interest is on furthering the understanding of the existence, stability, and bifurcation structure of localized steady-states to mathematical equations. This includes investigating localized structures in planar PDEs and in spatially discrete networked dynamical systems. Much of my work has focussed on how spatial dimension and organization can effect the existence regions of these patterns in parameter space. I am particularly interested in solutions that exhibit nontrivial symmetries, such as clusters of spots/bumps that self-organize to form hexagons on the macroscopic scale (see left image). A summary of some of my contributions in this area can be found in this video.